【算法】10.2青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：2

示例 2：

输入：n = 7
输出：21

示例 3：

输入：n = 0
输出：1

提示：

0 <= n <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/qing-wa-tiao-tai-jie-wen-ti-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

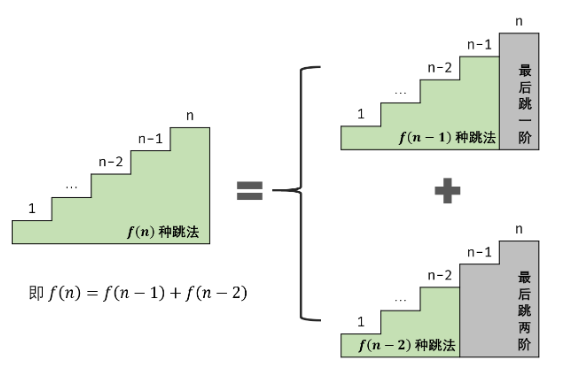
设跳上 n 级台阶有 f(n) 种跳法。在所有跳法中，青蛙的最后一步只有两种情况： 跳上 1 级或 2 级台阶。

• 当为 1 级台阶： 剩 n-1个台阶，此情况共有 f(n-1)种跳法；
• 当为 2 级台阶： 剩 n-2 个台阶，此情况共有 f(n-2) 种跳法。

f(n) 为以上两种情况之和，即 f(n)=f(n-1)+f(n-2) ，本题就转变为斐波那契数列了。

int numWays(int n)
{
    unsigned f0 = 1, f1 = 1, f2 = f0 + f1;
    int a = 1e9 + 7;

    if(n < 2)
        return 1;

    for(int i = 0; i<n-1; ++i)
    {
        f2 = (f0 + f1) % a;
        f0 = f1;
        f1 = f2;
    }
    return f2;
}